Introduction to Descriptive Statistics In Data Science
There are two types of statistics available first descriptive statistics in data science and second Inferential statistics. By which we can analyze data with the help of methods. Statistics is art about creating and contemplating
strategies for gathering, examining, organizing, and showing data paths.
Statistics is a science that finds its place virtually in all science and research fields in order to manage and improve data. Statisticians have been using different mathematical and computational tools to study this science.
Descriptive statistics in data science form the building blocks of data science, machine learning, and automation. In this learning tutorial, we will cover the basics of statistics and probability in data science.
Two basic ideas in the science of statistics are uncertainty and variation.
Instances are numerous in science and life wherein we are uncertain about the outcome. Sometimes, this uncertainty is also because the outcome has not been determined yet. A perfect example is that we don’t know if it will rain tomorrow. There are even cases when an outcome is there but the causes are uncertain. For example, it’s raining today, but the weather experts had forecasted a sunny day.
So, this uncertainty has resulted in the term “probability”. A probability is a mathematical tool or let’s say, language that is used to discuss uncertain events or causes. This probability plays the most important role in statistics. Every measurement or collection of data comes with a small margin of correction. We call it variance in mathematics. So, if we collect or measure the same data again, we may get variation in the outcome compared to the last ones.
Questions Of Descriptive Statistics in Data Science
Data Science is the one that analyzes the data and makes predictions. But the basis of this theory lies in the techniques that a data scientist uses to analyze that data to make predictions further. So, a data scientist first tries to understand the data by applying descriptive statistics in data science involves summarizing and organizing the data so they can be easily understood. Descriptive statistics in data science, unlike inferential statistics, seeks to describe the data but does not attempt to make inferences from the sample to the whole population.
Here, we typically describe the data in a sample. This generally means that descriptive statistics, unlike inferential statistics, is not developed on the basis of probability theory. Descriptive statistics in data science is more efficient than inferential statistics. By doing that a data scientist gets a fair idea of the type of distribution a particular data has. After all, he can apply algorithms and make some fancy predictions.
What is Descriptive Statistics in Data Science?
Descriptive statistics in data science involves summarizing and organizing the data so they can be easily understood. Descriptive statistics, unlike inferential statistics, seeks to describe the data but does not attempt to make inferences from the sample to the whole population.
Here, we typically describe the data in a sample. This generally means that descriptive statistics, unlike inferential statistics, is not developed on the basis of probability theory. Descriptive statistics in data science is more efficient than inferential statistics.
What Are The Types Of Descriptive Statistics In Data Science?
Descriptive statistics in data science are broken down into two categories:-
- Measures of central tendency
- Measures of variability (spread)
What Is The Measure Of Central Tendency?
Central tendency refers to the idea that there is one number that best summarizes the entire set of measurements, a number that is in some way “central” to the set.
- Mean/ Average
Mean or Average is a central tendency of the data i.e. a number around which a whole data is spread out. In a way, it is a single number that can estimate the value of the whole data set.
In school, we have read that average is simply the sum of all the events divided by the number of events. Let’s calculate the mean of the data set having 10 integers.
Mean/Average = 1+2+3+4+5+6+7+8+9+10/10 - Median
The median of the data is the middle figure in the set in Descriptive statistics in data science. We can also say that the median is also the number that is halfway into the set. The data should be first arranged in order from least to greatest. Note: If we sort the data in descending order, it will have no effect on the median, but IQR will become negative. That is another statistics term that we will discuss later in this tutorial. Median will be the middle term if the number of terms is odd
So, median of these numbers: 1+2+3+4+5+6+7+8+9+10+11 = 6
The Median will be the average of the middle 2 terms if the number of terms is even.
So, median of these numbers: 1+2+3+4+5+6+7+8+9+10 = sum of two middle terms = 5+6 and their average is 11/2 = 5.5 - Mode
Mode is a term that appears the maximum number of times in a data set according to descriptive statistics in data science. In mathematical terms, the Mode of a data set is the one that has got the highest frequency.
Example :- Calculate Mode of {1,2,3,4,4,6,5,1,5,6,4,8,2,4,8,7,5,2,4,7}
The mode for the above data set is 4 because its frequency is 5.
But If there’s the same distribution for 5 and 4 in the above data and frequency for both is 4 then this data set will be Bimodal because If two values appeared same time and more than the rest of the values then the data set is bimodal same as If three values appeared same time and more than the rest of the values then the data set is trimodal and for n modes, that data set is multimodal.
What is the measure of Spread / Dispersion?
Measures of spread describe how similar or varied the set of observed values are for a particular variable (data item) in descriptive statistics in data science. Measures of spread include the range, quartiles and the interquartile range, variance, and standard deviation.
A low standard deviation indicates that the data points tend to be close to the mean of the data set, while a high standard deviation indicates that the data points are spread out over a wider range of values.
In the case of individual observations, Standard Deviation can be computed in any of the two ways:
- Take the deviation of the items from the actual mean
- Take the deviation of the item from the assumed mean
In the case of a discrete series, any of the following methods can be used to calculate Standard Deviation:-
- Assumed mean method
- Step deviation method
Calculate the standard deviation for the following sample data using all methods: 2, 4, 8, 6, 10, and 12.



- Mean Deviation / Mean Absolute Deviation
It is an average of absolute differences between each value in a set of values, and the average of all values of that set in Descriptive statistics in data science. - Variance
The variance measures how far each number in the set is from the mean. Variance is calculated by taking the differences between each number in the set and the mean, squaring the differences (to make them positive), and dividing the sum of the squares by the number of values in the set. - Range
The range is one of the simplest techniques of descriptive statistics in data science. It is the difference between the lowest and highest values of data.
Max – min = range - Interquartile range (IQR)
Percentile is a way to represent the position of a value in a data set according to descriptive statistics in data science. To calculate percentile, values in the data set should always be in ascending order. When a data set has outliers or extreme values, we summarize a typical value using the median as opposed to the mean. When a data set has outliers, variability is often summarized by a statistic called the interquartile range, which is the difference between the first and third quartiles.The first quartile, denoted Q1, is the value in the data set that holds 25% of the values below it. The third quartile, denoted Q3, is the value in the data set that holds 25% of the values above it. The quartiles can be determined following the same approach that we used to determine the median, but we now consider each half of the data set separately
- Quartiles
A percentile is a comparison score between a particular score and the scores of the rest of a group in Descriptive statistics in data science. It shows the percentage of scores that a particular score surpassed. For example, if you score 75 points on a test, and are ranked in the 85th percentile, it means that the score of 75 is higher than 85% of the scores.The percentile rank is calculated using the formula :
R = P*(N)/100
where P is the desired percentile and N is the number of data points - Standard Deviation
The standard deviation formula stands for both sample and population despite being similar they are not the same. The symbol of the sample standard deviation formula would be – “s” (lowercase), population standard deviation symbol would be – “σ” (sigma, lowercase). Let’s take an example x is the number then = “x- mean” will be the deviation. It is used to calculate the standard deviation X = sum/n.
What Are Skewness In Descriptive Statistics In Data Science?
The measure of skewness determines the extent of asymmetry or lack of symmetry according to descriptive statistics in data science. A distribution is said to be asymmetric if its graph does not appear similar to the right and to the left around the central position. In more statistical language, the skewness measures how much is the asymmetry of the probability distribution of some given real-valued random variable about the mean.
Skewness can be observed in the given data when the number of observations is less. It is also known as two types of skewness: first Positive skew and second Negative skew.
For Example: When the numbers 9, 10, 11 are given, we may easily inspect that the values are equally distributed about the mean 10. But if we add a number 5, so as to get the data as 5, 9, 10, 11, then we can say that the distribution is not symmetric or it is skewed.
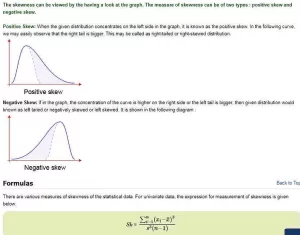
The skewness can be viewed by having a look at the graph. The measure of skewness can be of two types: positive skew and negative skew.
Positive Skew: When the given distribution concentrates on the left side of the graph, it is known as the positive skew. In the following curve, we may easily observe that the right tail is bigger. This may be called a right-tailed or right-skewed distribution in descriptive statistics in data science.
To calculate the skewness coefficient of the sample, there are two methods:
- Pearson First Coefficient of Skewness (Mode skewness)
- Pearson Second Coefficient of Skewness (Median skewness)
Interpretations:-
- The direction of skewness is given by the sign. A zero means no skewness at all.
- A negative value means the distribution is negatively skewed. A positive value means the distribution is positively skewed.
- The coefficient compares the sample distribution with a normal distribution. The larger the value, the larger the distribution differs from a normal distribution.
Sample problem: Use Pearson’s Coefficient #1 and #2 to find the skewness for data with the following characteristics:
- Mean = 50.
- Median = 56.
- Mode = 60.
- Standard deviation = 8.5.
Pearson’s First Coefficient of Skewness: -1.17.
Pearson’s Second Coefficient of Skewness: -2.117.
The measure of skewness is applied very commonly since skewed data is seen quite often in different situations. In commerce, the skewness has to be measured very frequently when incomes are skewed to the right or to the left.
On the other hand, the data which describes the lifetime of some commodities such as a tubelight, is right-skewed. The smallest lifetime may be zero, whereas the long-lasting tube lights will provide positive skewness to the distribution.
What Is Kurtosis In Descriptive Statistics In Data Science?
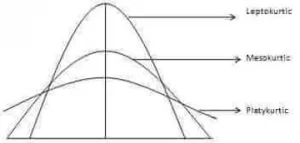
The degree of tailedness of a distribution is measured by kurtosis. It tells us the extent to which the distribution is more or less outlier-prone (heavier or light-tailed) than the normal distribution. Three different types of curves, courtesy of Investopedia, are shown as follows.
Descriptive statistics in data science for the beginners
It is difficult to discern different types of kurtosis from the density plots (left panel) because the tails are close to zero for all distributions. But differences in the tails are easy to see in the normal quantile-quantile plots (right panel).
The normal curve is called the Mesokurtic curve. If the curve of distribution is more outlier prone (or heavier-tailed) than a normal or mesokurtic curve then it is referred to as a Leptokurtic curve. If a curve is less outlier prone (or lighter-tailed) than a normal curve, it is called a platykurtic curve. Kurtosis is measured by moments and is given by the following formula.
The main difference between skewness and kurtosis is that skewness refers to the degree of symmetry, whereas kurtosis refers to the degree of presence of outliers in the distribution.
What Is Correlation In Descriptive Statistics In Data Science?
Correlation is a statistical technique in descriptive statistics in data science that can show whether and how strongly pairs of variables are related.
Correlation – (image)


The main result of a correlation is called the correlation coefficient (or “r”). It ranges from -1.0 to +1.0. The closer r is to +1 or -1, the more closely the two variables are related. If r is close to 0, it means there is no relationship between the variables. If r is positive, it means that as one variable gets larger the other gets larger. If r is negative it means that as one gets larger, the other gets smaller (often called an “inverse” correlation).
Conclusion
I hope, by now you have got a basic understanding of Descriptive statistics in data science. If you want to earn via Data Scientist as a career, enroll for our DataTrained Full Stack Data Science Course with Guaranteed Placement.